[칼럼] 수학 2등급~낮은 1등급, 기출 학습의 함정

출처 : https://orbi.kr/00067825009

[칼럼] 수학 2등급~낮은 1등급, 기출 학습의 함정 - 오르비

 

고정적으로 수학 2등급~낮은 1등급(주로 원점수 84~92)를 받는 학생들에게서

자주 보이는 문제점에 대해 이야기하려 합니다.

그건 바로 

 

     "기출 학습을 과신한다" 

 

얼핏 보면 이상한 말입니다.

3~4등급 때는 그렇게 죽어라 "기출해라 기출" 들었었는데,

갑자기 기출을 과신한다니 무슨 말인가 싶을 겁니다.

 

 

물론, 88점이나 92점까지 도달하는 과정에서 기출은 더할 나위 없이 중요합니다.

문제는 그 이후 2문제 정도에요.

 

 

남은 1~2문제는 이전 기출 학습이나 (개념) 내용 요소 학습으로 채워지지 않아요.

대표적으로

[211120]

 

 

[221121]

 

 

 

[231114]

 

 

 

[241122]

 

 

수능 출제만으로 봐도 이런 문항들이 있습니다.

 

92점의 벽을 넘어서 수학을 잘하는 학생들은 "이 문제들도 기출 잘 보면 당연히 풀 수 있는 거 아님?"

이라고 생각할 겁니다. 그리고 틀린 생각은 아니에요.

 

하지만 "수학적 센스", "새로운 문제에 대한 대응"을 둘 다 갖추지 못한 경우에는

실전에서는 이런 문제에서 턱턱 막히길 마련입니다.

 

예를 들어 위의 [221121] 문제를 생각해 봅시다.

당시 기준으로 이전 기출 문제에서 학습한 요소를 떠올려보면

 

(가)를 보고 "오, 초항은 ±2네. 이런 걸 다 알려주네"

(나)를 보고 "절댓값 취한 수열이 등비수열이네. 조건이 되게 쉬운데?"

이후 (다)를 보고 "합이 -14네"

 

그러고 나서 더 이상 조건을 분석할 게 없는 채로 문제가 끝났다는 것을 느끼게 됩니다.

 

여기서 센스가 좋은 친구들은

「뭔가 앞의 9개의 항이 마지막 항을 넘지 못하니까

부호는 항상 마지막 항이 결정하는 상황이 되겠다」

는 것을 눈치를 채고 풀이를 시작할 것이고,

새로운 상황이 주어졌을 때 분석을 잘하는 친구들은

「일단 a1=2라고 하고... 예를 들어서 전부 양수면 말이 안 될 테니까 

2, 4, -6, -8, ... , -512, 1024라 하면... 어? 1024가 있으면 앞에 합했을 때 어떻게 되는 거지?

-2, -4, ... , -512, 1024라 해도... 양수네?」

를 스스로 발견해내고 풀이에 접근할 수 있게 됩니다.

 

"기출을 과신" 한다는 것은 이런 부분에서의 표현입니다.

 

평가원은 거의 해마다, 이전에 물어본 내용적 요소에 더해 새로운 사고를 필요로 하는 문제를 내는데

새로운 사고를 필요로 하는 문제에 이전의 기출 문제에서 배웠던 상황을 끼워 맞추려는 것.

특히, 이전의 기출 문제에서 배웠던 상황과 일치하는 것이 없는데도 불구하고

다른 아이디어나 대입, 관찰 등의 시도를 하지 않고 포기하는 경우가 많습니다.

 

이런 문제들을 저는 국어의 열린 결말에 빗대어 열린 문제라고... 개인적으로 부르고 있습니다.

물론 수학 문제인 만큼, 진짜로 열린 답안이 나오는 것은 아니지만

이를 찾는 과정이 일반적인 문제들처럼 일방통행인 것이 아니고

주어진 조건이 뭔가 완결되지 않은 것 같지만 사실 어떤 이유로 정답은 몇 가지 밖에 될 수 없는 문제들

을 열린 문제라고 보면 될 것 같습니다.

 

너무 당연하고 쉬워서 다들 넘어간 문제겠지만,

a+b = 10 (단, a, b는 모두 짝수인 자연수)

도 열린 문제라고 할 수 있겠죠.

a+b가 10이 되는 실수의 순서쌍은 수없이 많지만, 짝수인 자연수라는 [상황 조건]이 있으니

정답은 한정된 몇 가지밖에 없는 것이죠.

 

 

그러면 이런 문제들은 어떻게 해결해야 할까요.

나는 수학적 센스도 없는 것 같고, 이것저것 대입해보고 관찰하기엔 시간도 부족한 거 같으니

이런 문제는 포기하자?

후자의 경우는 방향성이 명확합니다.

기출 학습 및 N제 연습을 통해서 다른 문제를 빨리 해결하는 연습을 해야 해요.

"시간만 더 있었다면, 대입 및 관찰을 충분히 해낼 수 있었다면 풀 수 있었을 텐데"

라고 생각하고 있다면 다른 문제에서 시간을 줄여야겠죠.

 

다만 수학적 센스라는 부분은 참 쉽지 않습니다.

선천적인 센스가 없다면, 후천적으로 센스를 키워야 하는데

이런 학습은 사실 조금 더 "수학 그 자체"에 가까운 학습에서 길러지는 부분이어서

PSS(문제해결전략, 모 강사의 책 말고 KMO 등 경시 대비용 책) 같은 책을 학습하는 게 오히려 낫겠지만...

PSS 같은 책을 두고두고 학습하려면 1년은 걸릴 테니까요. 

당장 수능이 있는데 1년이나 시간을 쓸 수도 없고.

 

 

그래도, 그나마 자주 다뤄지는 주제에 대해서 어떤 접근이 가능할지 정리해두는 정도는 필요하다고 생각해요.

 

(1) 극단적 케이스 상정

위의 [221121] 에서, 극단적으로 a9까지는 모두 음수고 a10만 양수여도 합이 양수인 것을 관찰한다든가,

주사위 5개를 던졌을 때 합이 29가 되는 상황이라고 하면

일단 5개가 다 6이면... 이라고 생각하는 흐름과 비슷합니다.

뭔가 조건이 부족하게 주어진 것 같은데 문제가 성립한다면

그런 극단적 케이스에서 시작을 해보는 것이죠.

 

(2) 집합 정보 확인하기 (~뿐이다 조건)

집합으로 조건이 주어진 경우, 자주 놓치는 조건이 있습니다.

 

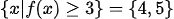
와 같이 조건이 주어졌다고 하면,

① f(x)가 3 이상이 되는 x 값이 4, 5이다   와 함께

② 4, 5를 제외한 x에서는 f(x)가 3 이상이 아니다

를 떠올려야 한다는 것이죠.

많은 학생들이 나머지 경우에서는 성립하지 않는다는 조건을 빼먹어서 답을 끝까지 만들어내지 못합니다.

수능에서 잘 출제되는 영역은 아니지만, 유한 집합이거나 범위가 정해져 있어서(유계인 집합)

최대·최소성을 물어보는 문제가 나올 수도 있지 않을까 싶기도 해요.

 

(3) 대입 및 관찰하기

얼핏 보면 규칙이 없는 수열이지만 대입해보니 주기가 생기거나,

변수가 k, t, a 등 다양하게 등장해서 상황에 대한 이해가 바로바로 어려울 때가 있습니다.

수열은 워낙 대입해서 찾는 문제가 많았으니 다들 잘하는 편이지만,

함수와 관련된 문제에서 변수가 많아지면 대입, 관찰을 통해서 상황을 이해하는 게 좋아요.

일반적인 경우를 한 번에 다루려고 하면 어떤 상황들이 생기는지 생각하기가 어렵기 때문이에요.

 

 

이 외에도 알고리즘에서 착안한 경우나, 도형 문제 등 다양한 영역이 있지만

새로운 문제 중 꽤 많은 비율은 이런 생각을 통해서 극복해낼 수 있지 않을까 싶습니다.

 

관련된 제작 문항도 2개 정도 올려두고 가겠습니다.

 

 

 

아마도 1번이 2번보다 어렵습니다